Comme vous pouvez le constater ci-dessous, dans les logiciels de bilan Exalang, les résultats aux différents subtests sont chiffrés en :
▪ Scores bruts
▪ Nombre d’écarts-types (Nbre d’E-T)
▪ Percentiles (P)
▪ Notes-Standard (N.S.)
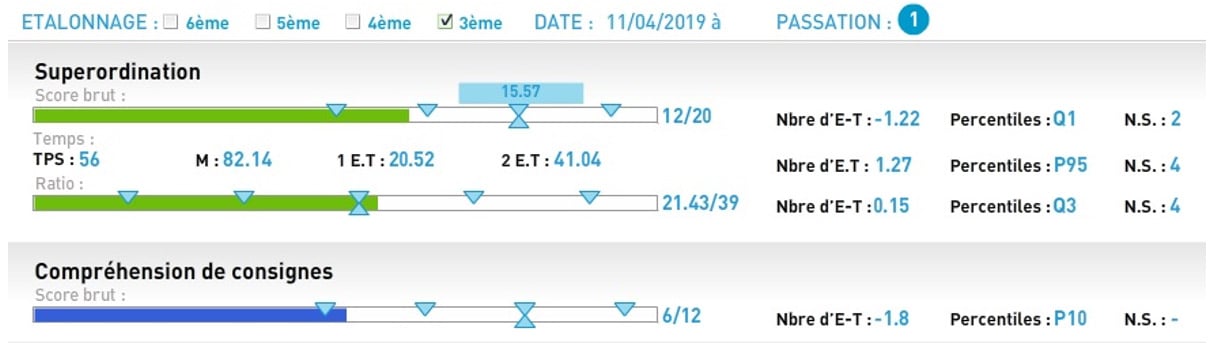
Dans cet article, nous allons détailler ces différentes valeurs et nous prendrons le temps d’expliquer comment les interpréter. Ce sera l’occasion de répondre à cette question récurrente sur la (non) correspondance des écarts-types et des percentiles.
Les différents scores et leur dispersion
Le score brut de réussite indique le nombre de bonnes réponses par rapport au score maximum de l’épreuve. Si vous passez votre souris sur les onglets triangles qui se font face, la moyenne obtenue par la cohorte à cette épreuve s’affichera (par exemple ici : 15.57 en Superordination). Les valeurs de -1 E-T et de -2 E-T ou de + 1 E-T et de +2 E-T s’obtiennent, quant à elles, en passant la souris sur les onglets triangles situés à gauche ou à droite de cette moyenne.
A noter que le score Temps n’est pas représenté par une barre colorée, mais sont notés numériquement : le temps brut, la moyenne et les valeurs 1 E-T et 2 E-T.
Le score Ratio détermine un seuil d’efficience en combinant le score de temps et le score brut. Il doit être interprété avec prudence, comme cela est indiqué dans les différents manuels Exalang. Succinctement, ce score comprenant deux variables, il peut être biaisé d’une part par l’augmentation du « bruit » (erreurs aléatoires de mesure cumulées) et d’autre part être rendu inexploitable par un comportement inadapté du sujet pendant la passation. Un ratio élevé chez un sujet performant correspondra en général à une bonne aisance tant au niveau du contenu que du temps de traitement, mais peut aussi correspondre, s’il est accompagné d’un score de réussite faible, à une trop grande impulsivité, un désintérêt de la tâche (réponses au hasard, sujet dispersé, stratégie inadaptée).
La moyenne d’une épreuve s’obtient simplement en divisant la somme des valeurs (scores) obtenue lors de l’étalonnage par le nombre de valeurs (sujets ayant passé l’épreuve).
L’E-T indique quant à lui le taux de dispersion de ces valeurs ; c’est en quelque sorte la moyenne des « distances à la moyenne ». Epargnons-nous sa formule de calcul. En revanche, nous reviendrons un peu plus loin sur sa (non) correspondance avec les percentiles.
NB : les plus impatient.e.s sont autorisé.e.s à se rendre directement au chapitre concerné
Percentiles : y’a des limites !
Les percentiles permettent d’ordonner les sujets, de les classer des « premiers aux derniers », mais sans spécifier la distance (l’écart) entre eux. Dans les Exalangs, pour tous les types de scores, les percentiles suivants sont indiqués (listés ci-après du moins performant au plus performant) : P5, P10, P25 (ou Quartile 1=Q1), P50 (ou Médiane = Med.), P75 (ou Quartile 3 = Q3), P90, P95.
Exemple : pour Superordination, le score brut est 12/20, ce qui correspond au percentile Q1 (ou P25).
Ci-dessous, extraites du manuel Exalang 11-15, sont indiquées les valeurs des limites des percentiles pour ce score :

Le terme « limites » a son importance ici pour bien comprendre la distribution des percentiles. C’est parce que notre patient avec son 12/20 (voir capture des résultats au début de l’article) a un score strictement inférieur à 14 (limite supérieure) et supérieur ou égal à 11 (limite inférieure) qu’il se situe en P25.
Considérons le cas de figure suivant : mon patient a obtenu 10/20 à cette épreuve. A quel percentile se situerait-il ? Non pas en P5, mais en P10, puisque 10 est bien strictement inférieur à « 11 » et supérieur ou égal à 10.
Dans les tableaux figurant dans les différents manuels, ce sont donc les limites des percentiles qui sont indiqués (et non pas que P5=10 ; P10 = 11 ; etc.). Si votre patient est par exemple, en P5 sur un score, c’est qu’il se situe nécessairement (strictement) en dessous du percentile 5.
De même, le percentile 50 (P50) ne correspond pas à la moyenne mais à la médiane. Qu’est-ce que la médiane ? C’est la valeur située au milieu d’une séquence ordonnée de valeurs. A moins d’avoir des valeurs égales (ce qui pourrait techniquement arriver lors d’un étalonnage où tous les sujets testés auraient obtenu la même note), la moitié des valeurs sera inférieure à la médiane et l’autre moitié supérieure à celle-ci. Il n’y a donc pas de correspondance stricte entre la moyenne et la médiane.
Allez, un peu de redondance ne fait pas de mal : quand un résultat est affiché en percentile 50, cela ne veut pas dire que ce résultat correspond exactement à la valeur unique du percentile 50, mais à la classe de résultats situés en dessous de la valeur du percentile 50 et au-dessus de la valeur du percentile 25 ; à savoir les résultats qui correspondent au deuxième quart de la distribution en partant des résultats les plus faibles.
D’accord, mais pourquoi P5 n’est-il pas toujours égal à -1.65 E-T ?
Vous avez certainement toutes et tous vu passer cette courbe que voici :
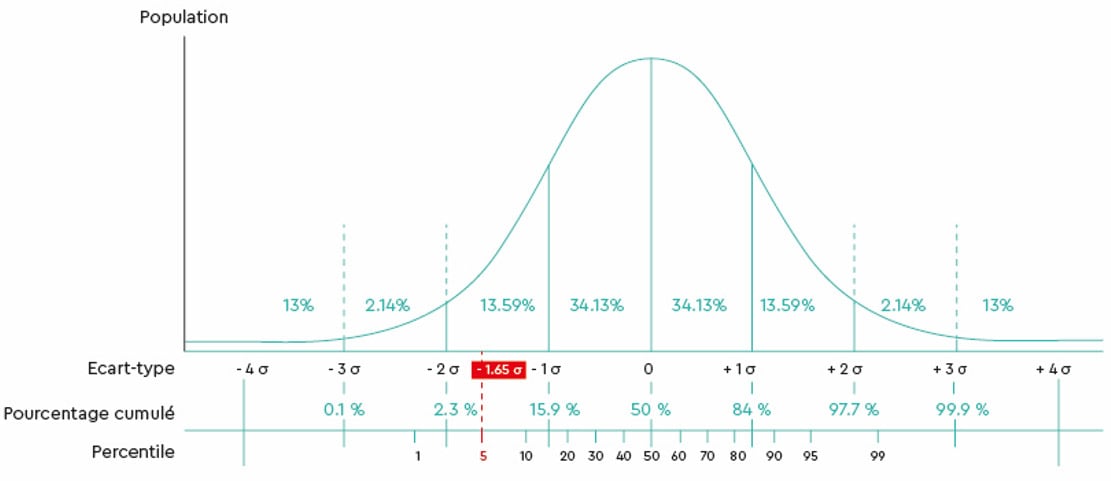
C’est la courbe de Gauss. Cette représentation en forme de cloche indique une distribution dite « normale » ou « de Gauss ». Nous pouvons constater que la majorité des sujets se situent au niveau de la moyenne, alors qu’à mesure qu’ils s’écartent de cette moyenne (que ce soit en « positif » ou en « négatif ») les sujets sont de moins en moins nombreux.
Comme on peut le voir dans ce graphique : quand la distribution des résultats à l'étalonnage est gaussienne, le P5 correspond à - 1,65 ET.
Or, nombre de résultats des Exalang ne suivent pas une courbe dite strictement gaussienne au niveau de leur distribution (c’est par ailleurs le cas dans de nombreux autres tests normés). Cela signifie que la distribution des résultats n’est pas équi-répartie de part et d’autre de la médiane. La correspondance théorique et mathématique entre Nombre d’E-T et valeur d’un percentile n’est alors pas respectée.
Ainsi : si la distribution n’est pas gaussienne, la limite du P5 peut être à -1.80 ou -1.43, etc. Il n’y a donc dans ce cas, pas de correspondance entre un nombre d’E-T et les pourcentages de sujets les plus faibles de la population de référence. Et cette non correspondance est évidemment effective pour tous les autres percentiles.
Les notes standard : un barème sur 5
Lorsque les résultats sont gaussiens, une note standard (N.S.) figure dans les résultats. Si un score est non gaussien, un tiret apparaît pour indiquer qu’aucune NS n’est disponible (c’est le cas en « compréhension de consignes » dans la capture des résultats supra).
Pour les Exalang, pour des questions de lisibilité, les NS ont été calculées sur une échelle à 5 classes. A chacune de ces 5 classes est affiliée une NS de 1 à 5 ; la note 3 correspondant à la classe centrée sur la médiane.
▪ NS 1 : correspond aux 6.7% de la population de référence ayant eu les résultats les plus faibles (≤ P6.7)
▪ NS 2 : correspond aux 24.2 % suivants de la population de référence (entre P6.7 et P30.9)
▪ NS 3 : correspond aux 38.2 % de la classe moyenne centrée sur la médiane (entre P30.9 et P69.1)
▪ NS 4 : correspond aux 24.2 % suivants de la population de référence (entre P69.1 et P93.3)
▪ NS 5 : correspond aux 6.7 % de la population de référence ayant eu les résultats les plus élevés (≥ P93.3)
Pourquoi des résultats ne suivent-ils pas la courbe de Gauss ?
Cela peut s’expliquer par :
▪ Un degré de dispersion des scores élevé.
▪ Un effet de saturation : un nombre important de sujets atteint le score maximum : les classes 4 et 5, voire parfois 3, 4 et 5 sont alors confondues.
▪ La nature intrinsèque de certaines épreuves, avec un type de notation qui ne permet pas la répartition en 5 classes ; typiquement pour les épreuves d’empan, avec une échelle réduite de notes.
Et on fait comment pour interpréter tout ça dans nos CRBO ?
Il est tout à fait intéressant de disposer des quatre notations : score brut, nombre d’écart-type, percentile et note standard.
La Note Standard présente l’avantage de situer « en un coup d’œil » le patient dans un groupe. La standardisation permet en effet de comparer facilement entre eux les résultats et de situer le patient testé par rapport à son groupe de référence. Mais il est nécessaire d’analyser les autres valeurs, que les séries soient gaussiennes ou non.
Pour l’interprétation, il est conseillé de se focaliser d’abord sur les percentiles :
▪ Dans la mesure où ils correspondent aux 5% les plus faibles, des résultats sous le P5 marquent des difficultés importantes.
▪ Mais des résultats répétés sous le P10 indiquent déjà des difficultés significatives qui peuvent signer un profil pathologique, en fonction aussi de l’analyse qualitative.
▪ A P25, les sujets sont dans une zone de fragilité. L’indication du Nbre d’E-T pourra alors permettre d’affiner l’analyse.
Pourquoi est-il intéressant de connaître la valeur de l’E-T ?
La valeur de l’E-T vous donne des indications par rapport à l’épreuve elle-même, sur le degré de dispersion des scores (c’est-à-dire des performances) dans la population de référence. Si l’E-T est grand, cela vous informe de la grande variabilité inter-individuelle dans la tranche d’âge (ou classe) concernée. Si, au contraire, l’E-T est faible, cela vous indique un niveau de performance homogène. Ainsi, les résultats du patient ne s’analysent pas pareillement, selon que l’épreuve présente des résultats plus ou moins homogènes dans la population de référence. Or cette information n’est pas donnée par les percentiles.
Conclusion : La lecture des résultats en percentiles est la plus « prudente » pour analyser les résultats du patient, quelle que soit la distribution (normale ou pas), d’autant plus quand des résultats sont proches des seuils. La connaissance de l’E-T est davantage intéressante pour comprendre comment l’épreuve est traitée par la population de référence.
Bien évidemment, à la lecture et interprétation des résultats quantitatifs, il est indispensable d’y ajouter une analyse qualitative (des réponses données, des stratégies observées et des éléments de l’anamnèse).



